决策树的划分依据一：信息增益

信息增益：以某特征划分数据集前后的熵的差值。熵可以表示样本集合的不确定性，熵越大，样本的不确定性就越大。因此可以使用划分前后集合熵的差值来衡量使用当前特征对于样本集合D划分效果的好坏。
信息增益 = entroy(前) - entroy(后)
注：信息增益表示得知特征X的信息而使得类Y的信息熵减少的程度

定义与公式
假定离散属性a有 V 个可能的取值:

假设离散属性性别有2（男，女）个可能的取值

若使用a来对样本集 D 进行划分，则会产生 V 个分支结点,

其中第v个分支结点包含了 D 中所有在属性a上取值为$a^v$的样本，记为$D^v$. 我们可根据前面给出的信息熵公式计算出$D^v$的信息熵，再考虑到不同的分支结点所包含的样本数不同，给分支结点赋予权重$\frac{|D^v|}{|D|}$

即样本数越多的分支结点的影响越大，于是可计算出用属性a对样本集 D 进行划分所获得的"信息增益" (information gain)

其中：

特征a对训练数据集D的信息增益Gain(D,a),定义为集合D的信息熵Ent(D)与给定特征a条件下D的信息条件熵$Ent(D|a)$之差，即公式为：

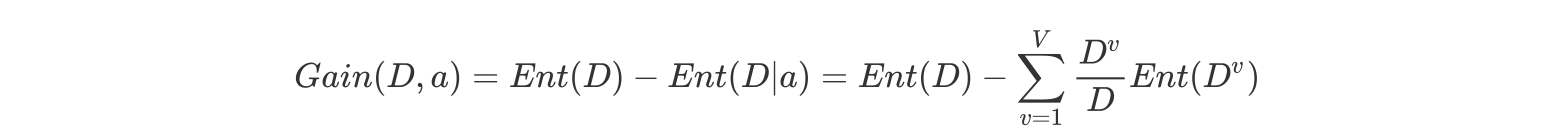
公式的详细解释：

信息熵的计算：

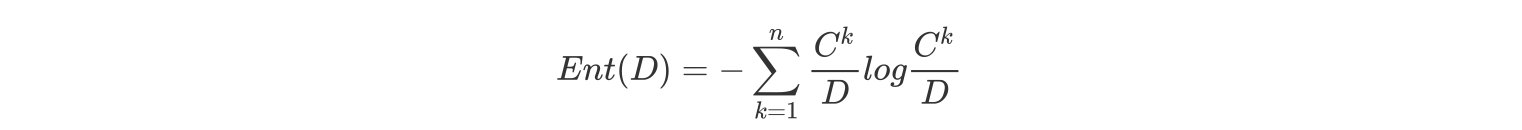
条件熵的计算：

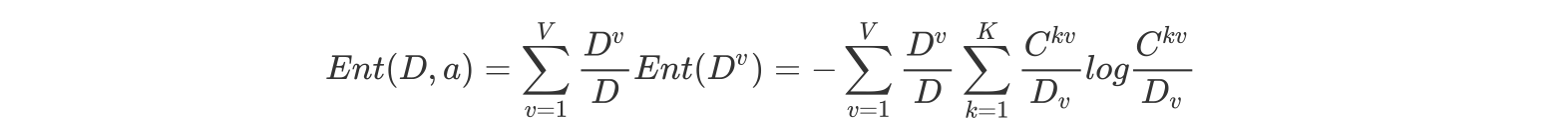
其中：

$D^v$ 表示a属性中第v个分支节点包含的样本数

$C^{kv}$ 表示a属性中第v个分支节点包含的样本数中，第k个类别下包含的样本数

一般而言，信息增益越大，则意味着使用属性 a 来进行划分所获得的"纯度提升"越大。因此，我们可用信息增益来进行决策树的划分属性选择，著名的 ID3 决策树学习算法 [Quinlan， 1986] 就是以信息增益为准则来选择划分属性。其中，ID3 名字中的 ID 是 Iterative Dichotomiser (迭代二分器)的简称


案例：

如下图，第一列为论坛号码，第二列为性别，第三列为活跃度，最后一列用户是否流失。

我们要解决一个问题：性别和活跃度两个特征，哪个对用户流失影响更大?

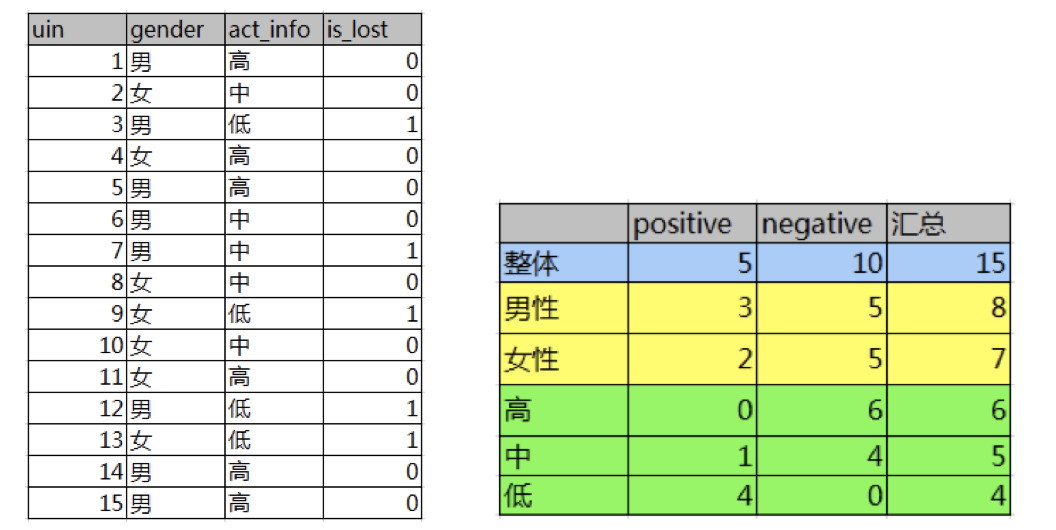
通过计算信息增益可以解决这个问题，统计上右表信息

其中Positive为正样本（已流失），Negative为负样本（未流失），下面的数值为不同划分下对应的人数。

可得到三个熵：

a.计算类别信息熵

整体熵：

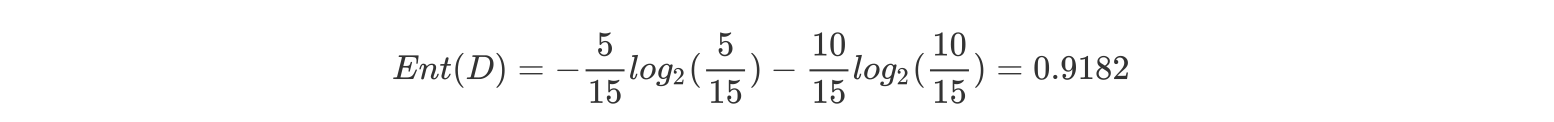
b.计算性别属性的信息熵(a="性别")

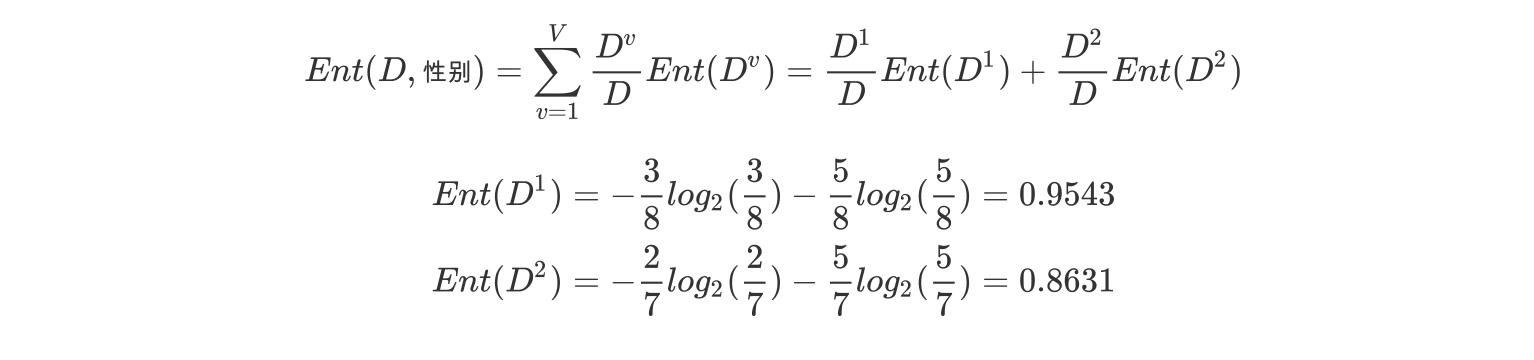
c.计算性别的信息增益(a="性别")

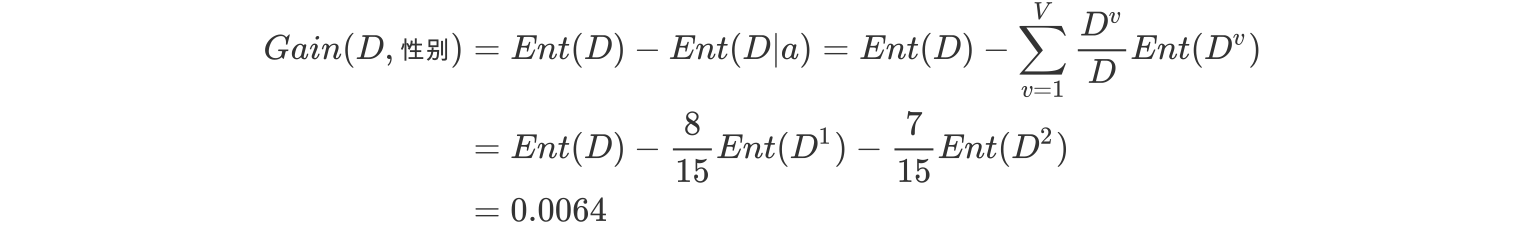
b.计算活跃度属性的信息熵(a="活跃度")

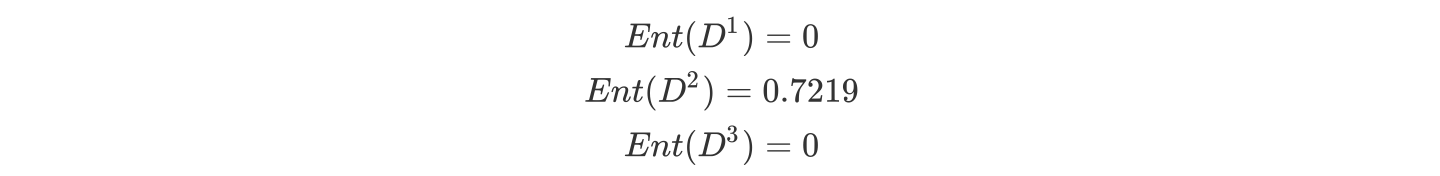
c.计算活跃度的信息增益(a="活跃度")

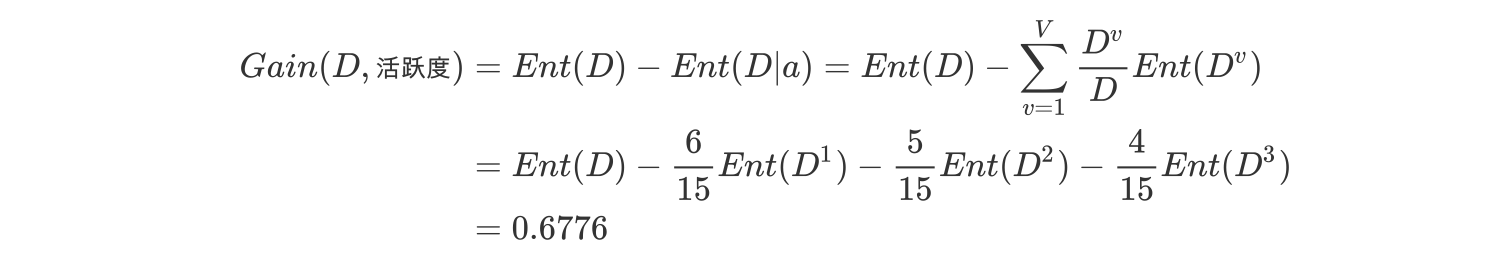
活跃度的信息增益比性别的信息增益大，也就是说，活跃度对用户流失的影响比性别大。在做特征选择或者数据分析的时候，我们应该重点考察活跃度这个指标。

meanshift算法原理：meanshift跟踪算法实战

Shi-Tomasi角点检测原理和实现代码

OpenCV图片相加和混合的方法【人工智能基础】

Shi-Tomasi角点检测原理和实现代码

传智教育ai人工智能课程